TRAPPIST-1

On Feb. 22 2017, astronomers announced the discovery that 7 Earth-sized planets orbit a nearby red dwarf star known as TRAPPIST-1, (Gillon et al 2017, Luger et al 2017). At least two of them should have the right temperatures to host liquid water making them prime targets in the search for life beyond the solar system.

The planets of TRAPPIST-1 are locked in the longest known chain of resonances ever discovered, with each planet’s orbital period forming simple ratios with those of its neighbours. For every 2 orbits of the outermost planet, the next planet inward orbits 3 times, the next one 4, then 6, 9, 15 and 24 times. We have recently shown in a research paper that the planets can settle into this configuration while drifting in their birth disk, and this fine tuning is likely the main reason the system has managed to survive to the present day (Tamayo et al. 2017).

Since musical harmony and repeating rhythms are also a result of simple period ratios, the orbits of the TRAPPIST-1 planets can be translated into musical form. For each planet, we play one note per orbit using the pitches that result from bringing the planet’s frequencies into the human hearing range. We then add drums for every time a planet passes its neighbour to hear the rhythms of their repeated gravitational tugs. To add a little more flair, we converted the fluctuating brightness data of the star itself directly into sound. Continue reading to learn about the creation of each element of TRAPPIST Sounds or play TRAPPIST-1 for yourself!

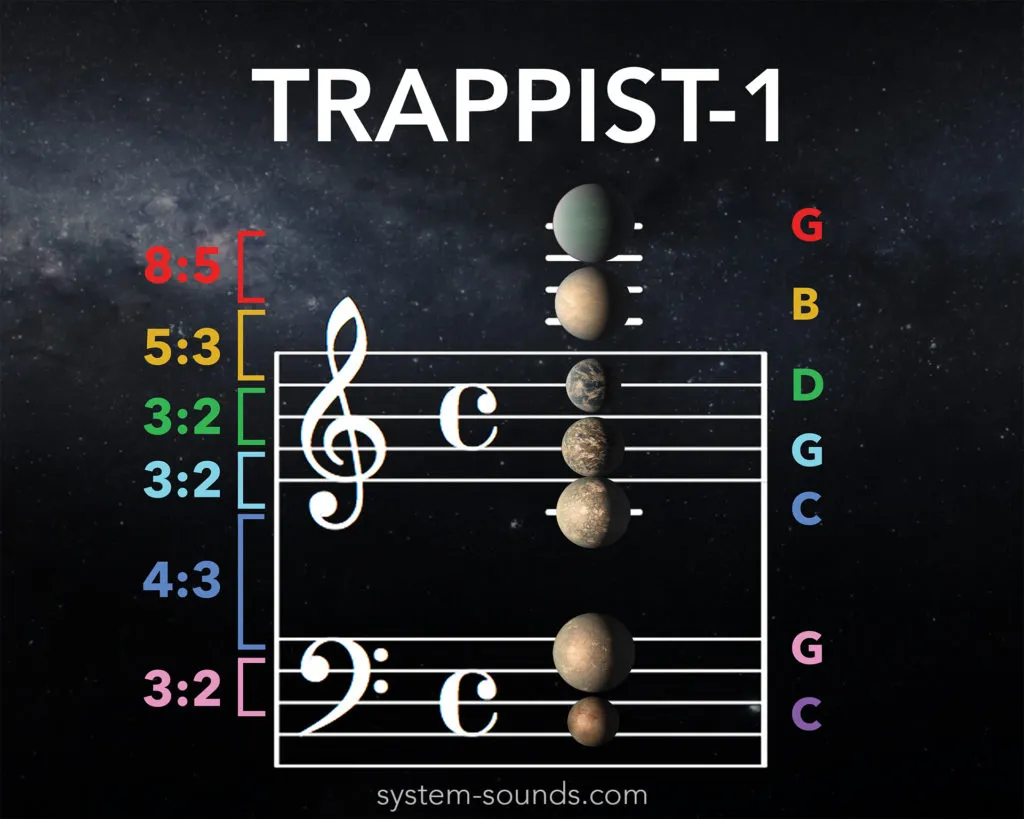
The simple period ratios of the TRAPPIST-1 planets create musical harmony when played as sound waves.

Trappist Melody

To translate the motion of the TRAPPIST-1 planets into music we developed custom software that anyone can use to bring their own systems to life, using the state of the art orbital integrator REBOUND. REBOUND simulates the TRAPPIST-1 system and records the times when each planet passes in front of the star from the Earth’s point of view (in the animation, the Earth is located 39 light years away off the right of the screen). The repeating pattern of ‘transits’ was in fact used to discover the planets of TRAPPIST-1. We then scaled time so that TRAPPIST1-h completes its orbit once every 2 seconds, which corresponds to a tempo of 30 bpm.

The actual orbital periods and corresponding frequencies and notes for each planet after scaling the orbital frequencies into the human hearing range. The resonances are written as the ratio of orbital frequencies (planet g orbits 3 times for every 2 orbits of planet h). Each resonance creates its own musical interval. (P5=perfect 5th, P4=perfect 4th, M6=major 6th and m6=minor 6th)

To assign a pitch to each planet we scaled the orbital frequencies into the human hearing range so that TRAPPIST-1h completes its 18.76 day orbit 130.81 times each second (130.81 Hz). This is equivalent to speeding up time by about 212 million times and the resulting note is known as C3. Since the frequencies of the interior planets are related to this ‘fundamental’ frequency by simple whole number ratios, they create a consonant harmony of stacked musical intervals. In fact, the orbital frequencies are not exactly whole number ratios and this discrepancy causes some notes to sound slightly out of tune, giving TRAPPIST-1 its own distinctive signature. If you’d like to create your own remix, download the MIDI file here (please credit system-sounds.com with all use).

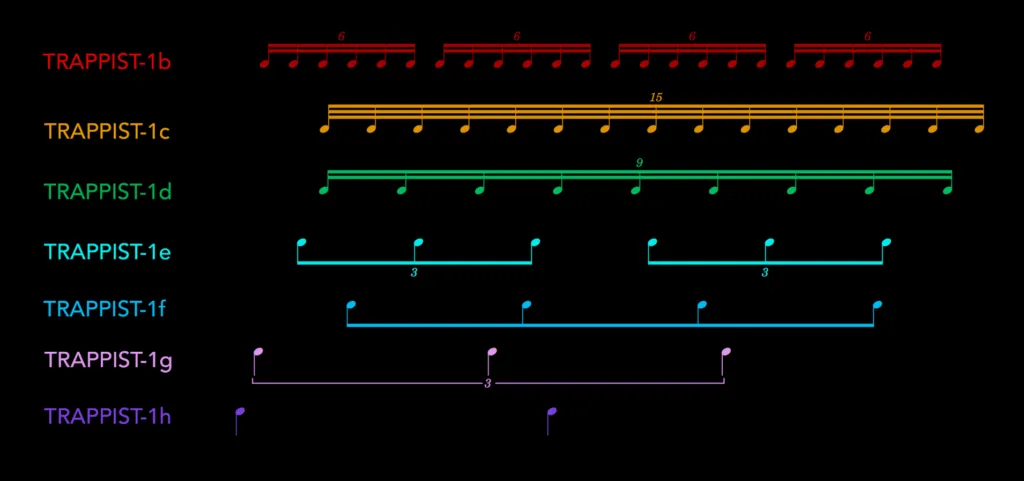
The rhythmic subdivisions of the transiting TRAPPIST-1 planets. The resonances are clearly visible (ex. there are 3 notes of TRAPPIST-1g for every 2 notes of TRAPPIST-1h). The patterns have been shifted to show their actual relative timing.

The key to TRAPPIST-1’s musical nature is that every planet is in resonance with its neighbours so that the whole system forms a harmonic resonant chain. Most planetary systems do not contain any planets in resonance and so when their motion is converted into sound the result is less than pleasing. It’s also important that there isn’t too large of a range between the periods of the outer and inner planets. As an example, we applied the same process used to make TRAPPIST Melody to the Kepler 90 system which also has 7 planets. Some of the planets are nearly in resonance but the wide range of orbital periods is translated to a painfully wide range of audio frequencies. Click below to hear the anti-TRAPPIST.

Trappist Beat

The gravitational tug between planets is greatest when they reach mutual conjunction, i.e., when a faster inner planet overtakes its outer neighbour. TRAPPIST Beat is created by assigning a different drum to conjunctions of each adjacent pair of planets. This rhythm is related to the pulses of TRAPPIST Melody but is more sparse since the proximity of the planets to one another, and thus their similar orbital speeds, means that each planet may complete several orbits (and transits) before passing one of its neighbours. Resisting the urge to use trap-style drums, we assigned each pair of planets to a different element of a standard drum kit, starting with a kick drum for every conjunction of planets g and h. Click here to download the midi file. (Please credit system-sounds.com with all use). You can find the code used to generate the basic video and MIDI files here.

An interesting pattern is visible if you look closely at the conjunctions. The outer 4 pairs of planets are in 1st order resonances (3:2, 4:3, 3:2, 3:2), which means that the inner planet does one more obit than the outer one for every resonant cycle. This implies that the inner planet only overtakes the outer planet once in this time, and then the cycle approximately repeats. It explains why these conjunctions in the movie (highlighted by lines in the animation) occur at approximately the same position every time, with slight drifts because the planets are not at exact resonance. The variations in conjunction positions carry information about the planets’ masses, as well as the ellipticities and alignments of their orbits.

But TRAPPIST-1c and TRAPPIST-1d are in a 2nd order 5:3 resonance so c overtakes d twice in a cycle, and their conjunctions (orange) can be seen occurring at opposing sides of the star. The innermost pair of planets is in a 3rd order 8:5 resonance which explains why their conjunctions (red) occur at 3 positions around the orbit.

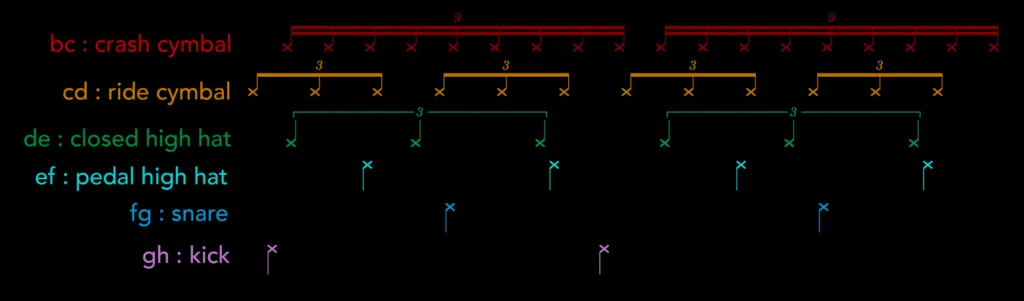
The rhythmic subdivisions of the conjunctions of TRAPPIST-1 planets with each pair of neighbouring planets assigned to a different drum. Again, the written patterns are shifted to show their actual relative timing.

Trappist Chord

The chord that swells after 45 seconds is created simply sustaining the pitches that correspond to each planet in TRAPPIST Melody. These notes are also doubled an octave lower, so that the lowest note is a C2, which causes a subtle throbbing beat pattern

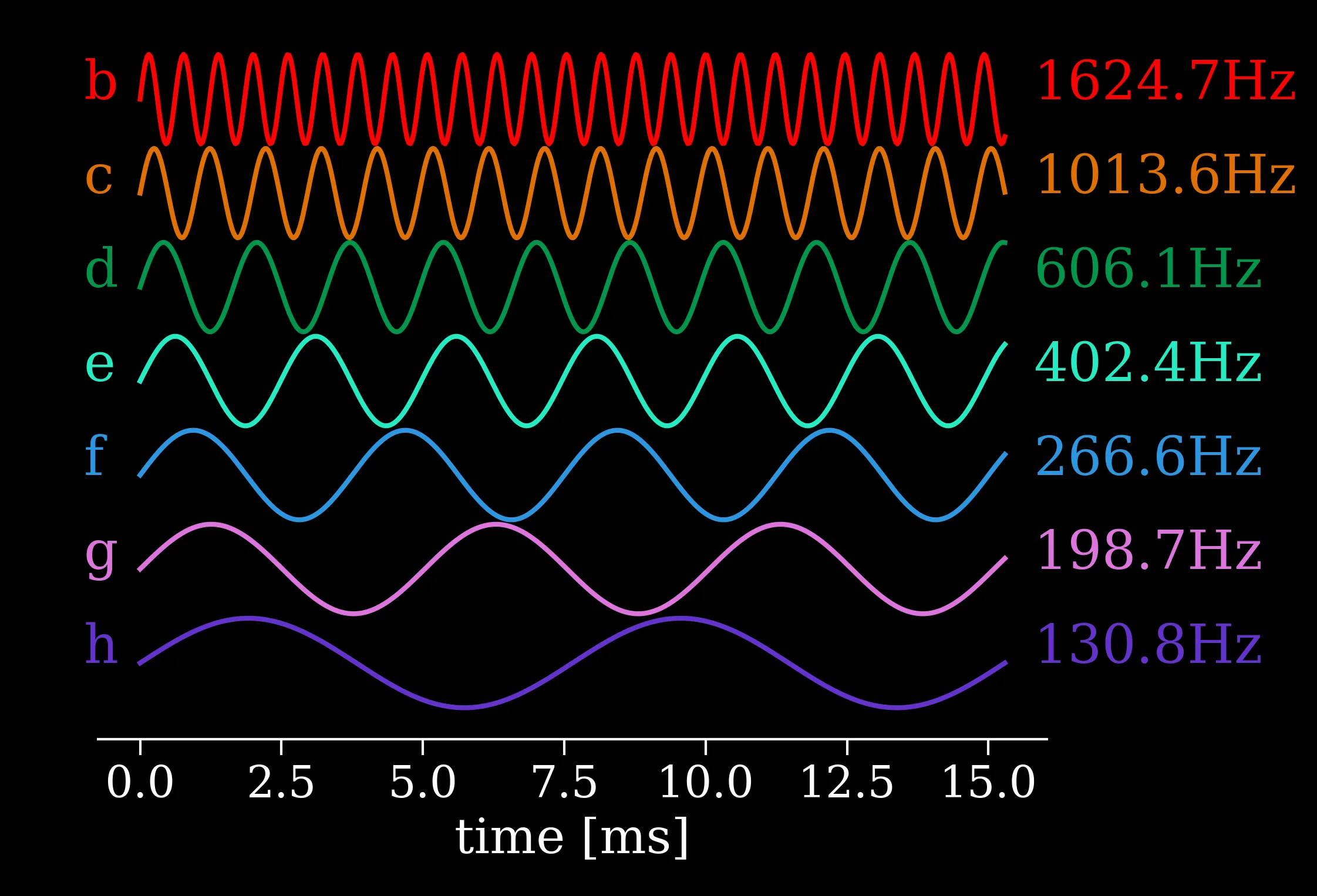
Sound waves with frequencies determined by scaling the planets’ orbital frequencies into the human hearing range. We set the outermost planet to a C note (130.81 Hz) and let physics do the rest. You can also see the resonances here, for example, 3 full wavelengths of planet g occur for every 2 wavelengths of planet h. Letters on left of image refer to planet names, not note names.

The scaled up frequencies of the TRAPPIST-1 planets create a sharp and slightly out of tune Cmaj9(no 3) chord.

Trappist Noise

The observed brightness variations of the star at the center of the TRAPPIST-1 system provides a final musical element. We begin with the 1st window of the Kepler telescope’s K2 long cadence observations of TRAPPIST-1. The star’s 3.3 day rotation period is clearly visible towards the end of the data as a result of giant sunspots that rotate with the star and temporarily reduce the observed brightness. We then speed up time by the same factor that was used when assigning pitches to the planets. At this rate, the star rotates at a frequency of 745 Hz which is very close to F#5, right in between the notes of TRAPPIST-1b and TRAPPIST-1c. This adds some lydian harmony and effectively turns TRAPPIST Chord into Cmaj9#11 that still lacks a major 3rd. Many higher frequencies are present due to the star’s inherent variability and the occasional solar flare. Since these occur stochastically (and not at low integer multiples of the star’s rotation period) they produce a thick, noisy tone. This very short audio sample is then looped many times and low frequency artifacts due to the looping are removed.

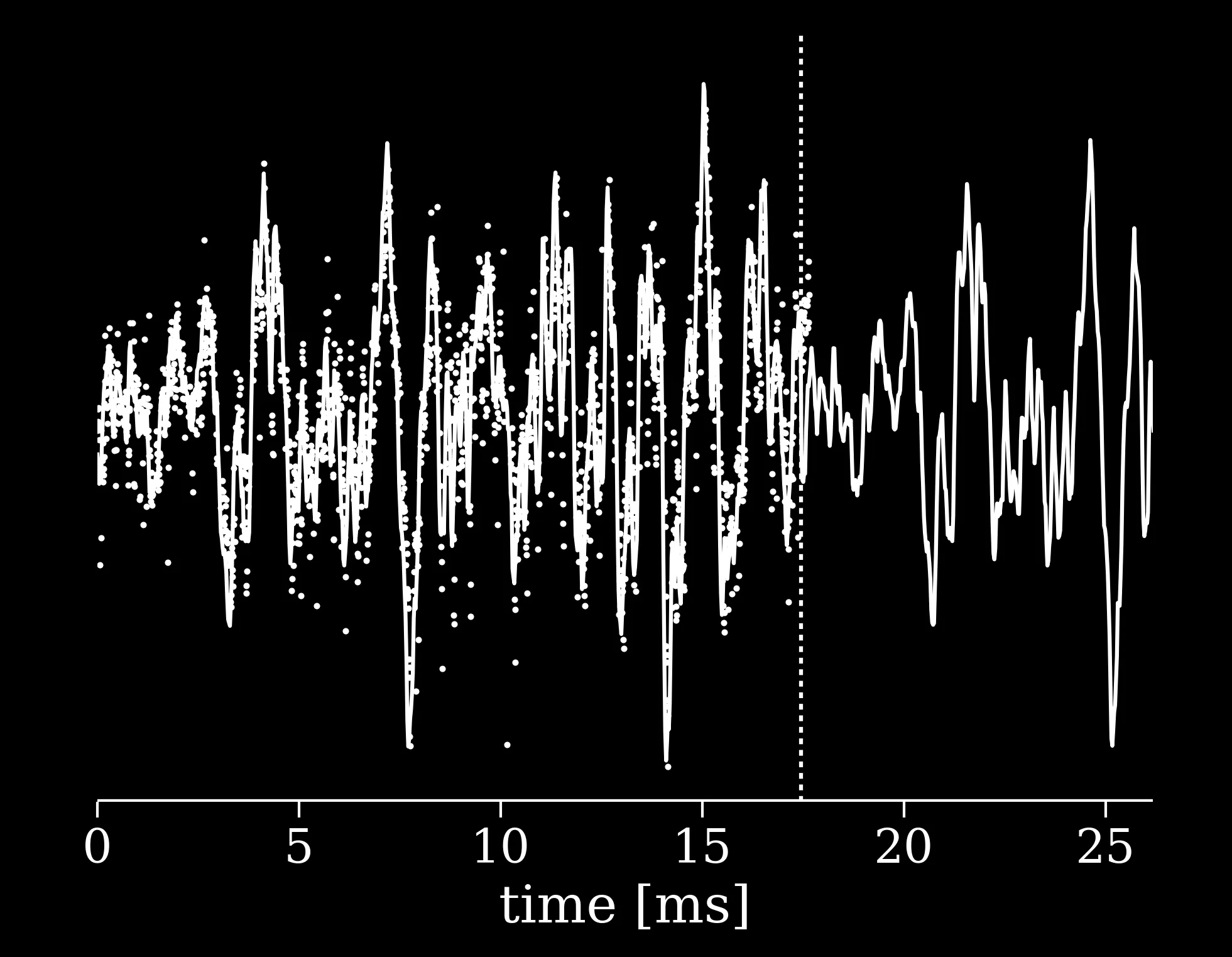
Finally, we used the same data of the star’s brightness variations to modulate the volume of this sound so that it is louder when the star is brighter. With this time scaling, the brightness/volume peaks occur almost 6 times for every orbit of TRAPPIST-1h, just as in real life. This produces the eerie crackling pattern that can be heard fading in towards the peak of TRAPPIST Sounds and continuing afterwards as the star recedes into deep space.